Red neuro-difusa para el relleno de datos faltantes en la estación meteorológica Chapingo
Network neuro-fuzzy for filling missing data in the meteorological station Chapingo
Juan Daniel Peña Durán
Centro Universitario UAEM Texcoco
texsmallville@hotmail.com
Irene Aguilar Juárez
Centro Universitario UAEM Texcoco
ireneico@gmail.com
Joel Ayala de la Vega
Centro Universitario UAEM Texcoco
joelayala2001@yahoo.com.mx
Resumen
Esta investigación presenta la aplicación de un modelo de red neurodifusa llamado ANFIS para el problema de estimación de datos faltantes meteorológicos: temperatura, velocidad del viento, humedad relativa y radiación solar en la estimación de la Evapotranspiración de referencia ETo. ANFIS es un método que permite crear la base de reglas de un sistema difuso, utilizando el algoritmo de retro propagación a partir de los datos de un proceso. La estructura de la red neuro-difusa para cada variable meteorológica consiste en dos entradas y una salida. La evaluación del relleno de datos faltantes se realiza mediante la Raíz Cuadrada del Error Cuadrático Medio (RMSE). Los resultados muestran que al usar un mayor número de iteraciones y variación de datos en el entrenamiento puede ayudar a la ANFIS a obtener resultados más precisos.
Palabras clave:ANFIS, datos faltantes, evapotranspiración de referencia.
Abstract
This research presents the implementation of a model called neurofuzzy ANFIS for the problem of missing data estimation weather: temperature, wind speed, relative humidity and solar radiation in estimating reference evapotranspiration ETo. ANFIS is a method for creating the rule base of a fuzzy system using the algorithm of retro spread from the data of a process. The structure of the network neurofuzzy for each meteorological variable consists of two inputs and one output. The evaluation of the filling of missing data is done by Square Root Mean Square Error (RMSE). The results show that using a higher number of iterations and data variation in training the ANFIS you can help to get more accurate results.
Key words:ANFIS, missing data, reference evapotranspiration.
Fecha recepción: Agosto 2014 Fecha aceptación: Diciembre 2014
Introducción
La Comisión Nacional del Agua (CONAGUA), a través del Servicio Meteorológico Nacional constituye la fuente oficial de datos meteorológicos y climáticos en México. El monitoreo y registro de dichos datos se realiza por medio de las Estaciones Meteorológicas Automáticas (EMAs), que están distribuidas alrededor de toda la República Mexicana. Sin embargo, la información de los registros meteorológicos en muchos casos está incompleta debido a diferentes factores, entre ellos: fallas en el funcionamiento y en la calibración del instrumental, en el mantenimiento de la estación y su instrumental. Por ejemplo, la estación meteorológica Chapingo, administrada por el Organismo de Cuenca Aguas del Valle de México (OCAVM, ubicada en el municipio de Texcoco, Estado de México, con coordenadas geográficas de latitud norte: 19° 50’ y longitud oeste: 98° 88’) realiza el monitoreo de diferentes variables meteorológicas pero en ocasiones los registros presentan ausencia de datos. Esta situación afecta la precisión de los resultados a la hora de efectuar cálculos importantes como la estimación de los requerimientos hídricos de los cultivos en las zonas de riego. No obstante, para satisfacer los requerimientos hídricos de los cultivos es necesario calcular la pérdida de agua producida por la evaporación y transpiración de los cultivos, por tal motivo la Organización Mundial de las Naciones Unidas para la Alimentación y Agricultura (FAO) en su Guía para las necesidades hídricas de los cultivos (Rivera, 2008) introduce el concepto de Evapotranspiración de cultivo de referencia (ETo), el cual estudia la tasa de evapotranspiración independientemente del tipo de cultivo y las características del suelo (Doorenbos & Pruitt, 1997).
Dada su definición, los factores que afectan la ETo son los factores climáticos, pudiendo ser calculada con parámetros climatológicos como temperatura, velocidad del viento, humedad relativa y radiación solar. Estos datos son proporcionados por las EMAs, pero como se mencionó anteriormente sufren de pérdida de datos cuyo efecto puede ser insignificante, pero cuando aumenta el tiempo de monitoreo con pérdidas de datos la base de datos se vuelve poco fiable. Para resolver el problema de los registros faltantes, la literatura propone el uso de diferentes técnicas, desde las tradicionales, como la regresión lineal, hasta las llamadas redes neuronales artificiales; pero a la hora de determinar qué modelo es más eficiente, algunos trabajos no encuentran diferencia entre los resultados. Por su parte, otros tienden a apoyar con ligera superioridad a las redes neuronales artificiales (Pitarque & Roy, 1998). De esa manera, para implementar alguna técnica debe considerarse la situación del entorno donde se va a desarrollar el estudio para obtener los resultados deseados.
Al respecto, cabe mencionar que la Estación Meteorológica Automática Chapingo carece de un historial de registro de datos de periodo de una hora de años anteriores, los datos obtenidos de la estación pueden presentar diferentes porcentajes de ausencia de datos; no se tiene algún otro parámetro que se relacione directamente con los datos medidos. Asimismo, no se pueden extrapolar los datos de una estación meteorológica próxima ya que se encuentran en peor situación, lo que limita las opciones de solución al problema. Por consiguiente, se considera utilizar la técnica de la lógica difusa ya que se puede trabajar con todos los registros completos e incompletos, y crear diferentes escenarios de acuerdo al comportamiento de cada variable meteorológica durante el año y el transcurso del día. Esto permite formular las reglas de inferencia, así como los conjuntos difusos para cada variable. El objetivo de este trabajo es diseñar y aplicar el modelo ANFIS para obtener un modelo aproximado del comportamiento de las variables meteorológicas, a partir de los datos registrados u obtenidos de la Estación Meteorológica Chapingo, y estimar datos perdidos.
El artículo está organizado de la siguiente forma: sección Antecedentes en donde se revisan trabajos relacionados con la recuperación de datos faltantes; sección Enfoque neurodifuso, en esta sección se muestran los elementos y relaciones que conforman la estructura de la red ANFIS; la sección Modelo propuesto a través de la ANFIS, presenta el modelado de los conjuntos difusos, los rangos de valores y funciones de nuestra red neurodifusa; sección Experimento y resultados, muestra la implementación de la red neurodifusa en el cálculo de la evapotranspiración y la estimación del RSME; por último, la sección Conclusiones y trabajos futuros, muestra un panorama general sobre las bondades del modelo ANFIS en la estimación satisfactoria de datos faltantes.
Antecedentes
En la literatura se han presentado diferentes aproximaciones al problema del relleno de datos faltantes dependiendo de la variable a completar en registros; en la investigación (Campos, Quispe, & Tatiana, 2012) se propone una metodología de gestión de datos meteorológicos para el trabajo sobre precipitaciones, así como la aplicación del método de llenado de la ecuación inversa de la distancia Euclidiana con la matriz de correlación si es que se presentan espacios. Los resultados fueron satisfactorios con la ecuación de la inversa de la distancia Euclidiana con la matriz de correlación, ya que permite una variación tanto dentro de la media como de las variaciones que se dan a lo largo del periodo de tiempo manejado. Sin embargo, el estudio concluye que durante la selección de estaciones se debe tener cuidado, seleccionando estaciones con coeficientes de correlación mayores a 0.75 y con porcentaje de vacíos menor al 20 %, lo que garantiza un llenado de datos confiable pues se tienen porcentajes de variación que oscilan del 0 al 15 %. En el presente escrito (Ferreira, 2003) se estudiaron diversos métodos de análisis e imputación de datos no completos, bajo el enfoque de su aplicación para completar los valores faltantes en series de velocidad del viento; sus resultados son interesantes para la velocidad del viento. En el trabajo descrito (R. Alfaro, Alfaro, & Pacheco, 2000) se muestran diferentes métodos para el relleno de vacíos en la serie anual de la precipitación aplicada a los registros de las estaciones meteorológicas, ubicadas en diferentes regiones de Costa Rica. Los métodos de relleno utilizados para reproducir una serie de datos estimados utilizando al menos una estación cercana a la estación en estudio son: regresión simple, de la razón, de la razón ajustada, regresión múltiple y de la razón normal. Los resultados del trabajo muestran diferencias máximas absolutas entre los valores reales y estimados de alrededor de 30 %, lo que sugiere la utilización de métodos más complejos de los presentados en dicho estudio si se desean hacer estimaciones más precisas de datos anuales de precipitación. La referencia (Valesani & Quintana, 2009) tiene por objeto la aplicación de una Red Neuronal Artificial (RNA) como método de imputación simulando porcentajes de ausencia de datos aplicando la técnica MCR (Missing Completely at Random). Después se evalúa su eficiencia en distintas situaciones con el propósito de valorar el comportamiento con distintos parámetros como MAE (Error Absoluto Medio), RMSE (Error Cuadrático Medio), y Regresión con la finalidad de conocer si las RNA son adecuadas para la imputación de datos en este caso en particular. Los resultados mostrados en la investigación son satisfactorios y se consideran aceptables en términos estadísticos. De igual manera, la propuesta (Solana & Bote, 1998) resalta las Redes Neuronales Artificiales mencionando conceptos técnicos, así como también las aplicaciones concretas en el campo de la recuperación de la información. En la propuesta (Cruz, 2012) se establece una metodología para el relleno de datos meteorológicos faltantes que se desarrolla en el entorno de programación Matlab usando la técnica de interpolación Piecewice Cubic Hermite Interpolating Polynomial (PCHIP) que ofrece el software. Para evaluar el desempeño de la interpolación se utiliza la raíz del cuadrado medio del error (RMSE). Cabe señalar que los resultados sobre el relleno de los datos ausentes no son presentados en ese trabajo. Para la resolución del problema de datos faltantes meteorológicos se han utilizado algunas técnicas tradicionales como la regresión, la homogeneidad de estaciones cercanas y el uso de las técnicas de Inteligencia Artificial más recientes, basadas en lógica difusa (aprendizaje inductivo), los algoritmos genéticos y las redes neuronales (Saba & Ortega, 2008), (Alfaro & Soley, 2009), (Chen, 1995); sin embargo, el problema surge cuando encontramos resultados contradictorios a la hora de determinar cuáles modelos son más eficientes en la solución del problema de falta de datos.
El presente trabajo de investigación ha considerado utilizar como técnica para rellenar los datos faltantes en la Estación Meteorológica Automática Chapingo a las redes neuro-difusas. De esa manera se refuerza el estudio de la Inteligencia Artificial en sistemas complejos y no lineales.
- Enfoque Neurodifuso
Las redes neurodifusas son sistemas que aprovechan características de las redes neuronales como la capacidad de aprender o auto ajustarse y generalizar, sumadas a las características de la lógica difusa, que trabaja con razonamiento lógico basado en funciones de membresía, que permiten trabajar con variables lingüísticas, muy naturales para los seres humanos. Los sistemas de inferencia difusos pueden representar el conocimiento basándose en reglas if-then, pero no tiene la capacidad de adaptarse cuando las condiciones externas cambian. Por este motivo, se incluyen los conceptos de reconocimiento de las redes neuronales.
La base de los sistemas neurodifusos se encuentran en las neuronas difusas, basadas en emular la morfología biológica de la neurona, seguida por un sistema de aprendizaje más la característica difusa. Podemos clasificar a las neuronas difusas en dos clases: en la primera, la característica difusa se encuentra en la descripción de los pesos sinápticos, y la segunda, las señales que se transmiten son difusas junto con los pesos sinápticos.
Hay que tener en consideración acciones muy importantes para el desarrollo de sistemas neurodifusos: a) definición de los valores de entrada y salida, b) definición de los conjuntos difusos que se requieran utilizar, c) definición de las reglas difusas, d) estructuración de la red neuronal y e) modelación de conexiones sinápticas que permitan incorporar interpretación difusa.
En las últimas décadas los sistemas neurodifusos se han posicionado en aplicaciones importantes en diferentes áreas tales como: control (en la mayoría de los sistemas); análisis cuantitativos (operaciones, manejo de datos); inferencia (sistemas expertos para el diagnóstico, planeación y predicción, procesamiento del lenguaje natural, robótica, ingeniería de software), y búsqueda y recuperación de información (base de datos), entre otras aplicaciones (Lin, Lee, & CS, 1996).
Por consiguiente, para esta investigación se decide modelar la dinámica del proceso a través del primer sistema neurodifuso conocido y el más establecido, ANFIS; además de ser uno de los trabajos pioneros, resulta uno de los más sencillos computacionalmente hablando (Jang., 1993). ANFIS implementa el modelo de Takagi-Sugeno para la estructura de las reglas If-then del sistema difuso. Un modelo ANFIS está conformado por cinco capas en la que todos los nodos de una misma capa tienen una función similar. La primera capa es usada para las entradas. La última capa para la salida y tiene 3 capas intermedias ocultas. Este número de capas ocultas permanece constante en todo tipo de ANFIS a implementar, sin importar las entradas que tenga el sistema y solamente tiene una salida posible. En la figura 1 se muestran las cinco capas de la red ANFIS y la relación entre nodos de entrada, variables lingüísticas, nodos de reglas, reglas normalizadas y parámetros, posteriormente se explica la función de la red capa por capa.
El comportamiento de cada capa de la ANFIS se describe a continuación:
Capa 1: Cada nodo i de esta capa es adaptable, es decir, tiene parámetros ajustables y descritos por la ecuación 1.
0i1= µAi(x) (1)
Donde x es la entrada al nodo i, Ai es una variable lingüística asociada con la función de este nodo. En otras palabras, 0i1 es la función de membresía de Ai y especifica el grado de pertenencia de x respecto a Ai.
Capa 2: Cada nodo en esta capa está etiquetado con Π (figura 1). En esta capa se multiplican las señales de entrada y se envía el producto a la salida, es decir, cuando múltiples señales entran a este nodo envían como resultado el producto de cada instancia i. Para un instante: 0i2 = µAi(x) µBi(y), i=1,2 (2)
Cada nodo de salida representa el grado de activación de una regla. Además, representan las T-norma o T-Conorma para modelar las operaciones lógicas AND y OR. Se suelen conocer como nodos de reglas.
Capa 3:Cada nodo etiquetado con N (figura 1), para indicar la normalización de los grados de activación. El i-ésimo nodo calcula la normal de las reglas de activación con la suma de todas las reglas activadas de acuerdo a la ecuación 3. Las salidas de esta capa pueden llamarse reglas de activación normalizadas.
 0i3= w1 = wi / wi+w2 (3)
0i3= w1 = wi / wi+w2 (3)
Capa 4:Cada nodo i en esta capa es cuadrado y tiene una función de nodo:

 0i4= wifi = wi(pix + qiy + ri), i=1,2 (4)
0i4= wifi = wi(pix + qiy + ri), i=1,2 (4)
 Donde wi es la salida de la capa 3 y el conjunto de parámetros {pi, qi, ri} son referidos a los parámetros de la consecuencia.
Donde wi es la salida de la capa 3 y el conjunto de parámetros {pi, qi, ri} son referidos a los parámetros de la consecuencia.
Capa 5:Presenta un nodo único circular con la etiqueta ∑, aquí se calcula la salida a partir de las señales de entrada (ecuación 5):

 0i5= f = ∑ wifi = ∑i wif / ∑iwi = wifi + w2f2 (5)
0i5= f = ∑ wifi = ∑i wif / ∑iwi = wifi + w2f2 (5)
El proceso de entrenamiento se realiza con dos conjuntos de parámetros: los del antecedente (constantes que caracterizan las funciones de pertenencia) y los de la consecuencia (coeficientes de las funciones lineales del consecuente de las reglas). Los enlaces entre nodos solo indican la dirección en la que fluyen las señales, no tienen pesos asociados (Villada F & García).
Modelo propuesto
Para implementar el ANFIS se utilizaron datos reales de series climáticas, las cuales obtenemos de la estación meteorológica Chapingo. Las variables meteorológicas se registraron a intervalos de 10 minutos durante periodos diarios de septiembre de 2013 hasta los días en curso. Las variables modeladas son velocidad del viento (VELS), temperatura (TEMP), humedad relativa (HR) y radiación solar (RAD-SOL). En el modelo neurodifuso se asignan las variables H (Hora) y Estación (EA) como variables de entrada y las variables meteorológicas velocidad del viento, temperatura, humedad relativa y radiación solar como variables de salida. Las variables Hora y Estación del Año son dependientes, mientras que velocidad del viento, temperatura, humedad relativa y radiación solar son dependientes de las dos primeras. Como valores lingüísticos de la H (Hora) se proponen: Madrugada (M1), Mañana (M2), Mediodía (M3), Atardecer (A1), Anochecer (A2) y Noche (N). El conjunto borroso para hora del día se muestra en el inciso A de la figura 2.
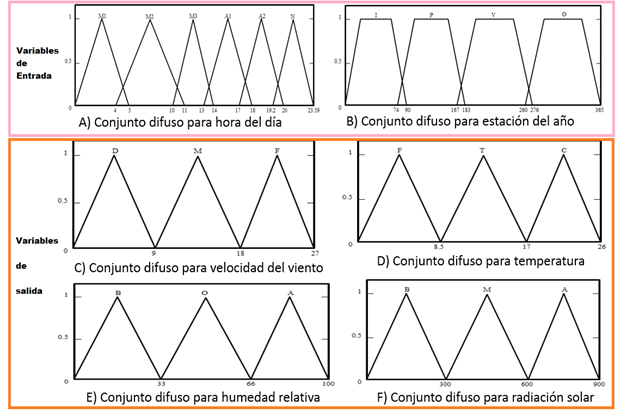
Figura 2: Conjuntos difusos para: a) hora del día, b) estación del año, c) velocidad del viento, d) temperatura, e) humedad relativa y f) radiación solar
Para no incurrir en estados pobremente definidos se utilizó un entrecruzamiento mínimo, considerando el comportamiento de las variables meteorológicas durante el día, de tal modo que cada elemento quede representado en al menos dos funciones de pertenencia. Se utiliza la función triangular para especificar el punto máximo de cada etiqueta lingüística.
Por la dificultad de establecer una escala homogénea en la duración de los meses del año, se decidió distribuir los días del año con base en las estaciones. De esta forma para este estudio el primer día del año se asignó al primer día de invierno, que es el 21 de diciembre y corresponde al día 90 la fecha 21 de marzo último día de invierno.
Como conjuntos difusos así como la etiqueta lingüística de la variable Estación del Año se proponen: Invierno (I), Primavera (P), Verano (V) y Otoño (O). La función de pertenencia de la variable Estación del Año se muestra en el inciso B de la figura 2. Se realizó un entrecruzamiento considerando el comportamiento de las variables meteorológicas pues en el cambio de estación del año en los días de inicio de una y los últimos días de la otra el comportamiento de la variable es semejante. Asimismo, se utilizó la función trapezoidal ya que dentro de las estaciones del año hay un lapso donde el comportamiento de las variables es estable y se mantiene durante un periodo.
Los rangos para las cuatro variables lingüísticas son: velocidad del viento [0, 27] en km/h, temperatura [0, 26] en C°, humedad relativa [0, 100] en % y radiación solar [0, 900] en Wm2. Los rangos se obtuvieron de valores promedio de cada estación del año. Los conjuntos difusos con sus respectivas etiquetas lingüísticas que conforman cada una de las variables fueron los siguientes: velocidad del viento [Débil (D), Moderado (M) y Fuerte (F)] ver inciso C de la figura 2; para temperatura [Frio (F), Templado (T), Cálido (C)] ver inciso D de la figura 2; para la humedad relativa [Baja (B), Moderada (M) y Alta (A)] ver inciso E de la figura 2 y radiación solar [Baja (B), Moderada (M) y Alta (A)] ver inciso F de la figura 2.
La forma de las reglas que se utilizan para Velocidad del Viento es como sigue: IF Estación es x AND Hora es y THEN VELS es z. Ver tabla I.
Tabla I. Reglas de inferencia para velocidad del viento.
# Regla |
Estación |
Hora |
VELS |
# Regla |
Estación |
Hora |
VELS |
1 |
I |
M1 |
D |
14 |
O |
M1 |
D |
2 |
I |
M1 |
M |
15 |
O |
M1 |
M |
3 |
I |
M2 |
D |
16 |
O |
M2 |
D |
4 |
I |
M2 |
M |
17 |
O |
M2 |
M |
5 |
I |
M3 |
D |
18 |
O |
M3 |
D |
6 |
I |
M3 |
M |
19 |
O |
M3 |
M |
7 |
I |
A1 |
D |
20 |
O |
A1 |
D |
8 |
I |
A1 |
M |
21 |
O |
A1 |
M |
9 |
I |
A2 |
D |
22 |
O |
A2 |
D |
10 |
I |
A2 |
M |
23 |
O |
A2 |
M |
11 |
I |
N |
D |
24 |
O |
N |
D |
12 |
I |
N |
M |
25 |
O |
N |
M |
13 |
I |
N |
F |
26 |
O |
N |
F |
Para Temperatura es de la forma IF Estación es x AND Hora es y THEN TEMP es z como se muestra en la tabla II.
Tabla II. Reglas de inferencia para Temperatura.
# Regla |
Estación |
Hora |
TEMP |
# Regla |
Estación |
Hora |
TEMP |
1 |
I |
M1 |
F |
15 |
O |
M1 |
T |
2 |
I |
M1 |
T |
16 |
O |
M1 |
C |
3 |
I |
M1 |
C |
17 |
O |
M2 |
T |
4 |
I |
M2 |
F |
18 |
O |
M2 |
F |
5 |
I |
M2 |
T |
19 |
O |
M3 |
T |
6 |
I |
M3 |
F |
20 |
O |
M3 |
F |
7 |
I |
M3 |
T |
21 |
O |
A1 |
F |
8 |
I |
A1 |
F |
22 |
O |
A1 |
T |
9 |
I |
A1 |
T |
23 |
O |
A1 |
C |
10 |
I |
A1 |
C |
24 |
O |
A2 |
C |
11 |
I |
A2 |
T |
25 |
O |
N |
C |
12 |
I |
A2 |
C |
26 |
O |
N |
T |
13 |
I |
N |
T |
|
|
|
|
14 |
I |
N |
F |
|
|
|
|
De igual forma, para Humedad Relativa es de la siguiente forma: IF Estación es x AND Hora es y THEN HR es z. Ver tabla III.
Tabla III. Reglas de inferencia para Humedad Relativa
# Regla |
Estación |
Hora |
HR |
# Regla |
Estación |
Hora |
HR |
1 |
I |
M1 |
B |
16 |
O |
M1 |
O |
2 |
I |
M1 |
O |
17 |
O |
M1 |
A |
3 |
I |
M1 |
A |
18 |
O |
M2 |
O |
4 |
I |
M2 |
B |
19 |
O |
M2 |
A |
5 |
I |
M2 |
O |
20 |
O |
M3 |
A |
6 |
I |
M2 |
A |
21 |
O |
A1 |
O |
7 |
I |
M3 |
O |
22 |
O |
A1 |
A |
8 |
I |
M3 |
A |
23 |
O |
A2 |
B |
9 |
I |
A1 |
B |
24 |
O |
A2 |
O |
10 |
I |
A1 |
O |
25 |
O |
A2 |
A |
11 |
I |
A1 |
A |
26 |
O |
N |
A |
12 |
I |
A2 |
B |
27 |
O |
N |
O |
13 |
I |
A2 |
O |
28 |
O |
N |
B |
14 |
I |
N |
B |
|
|
|
|
15 |
I |
N |
O |
|
|
|
|
Y por último, para Radiación solar es de la siguiente forma: IF Estación es x AND Hora es y THEN RAD-SOL es z. Ver tabla IV.
Tabla IV. Reglas de inferencia para Radiación Solar
# Regla |
Estación |
Hora |
RAD-SOL |
# Regla |
Estación |
Hora |
RAD-SOL |
1 |
I |
M1 |
B |
12 |
O |
M1 |
B |
2 |
I |
M2 |
B |
13 |
O |
M1 |
B |
3 |
I |
M3 |
B |
14 |
O |
M3 |
B |
4 |
I |
A1 |
B |
15 |
O |
A1 |
B |
5 |
I |
A1 |
M |
16 |
O |
A1 |
M |
6 |
I |
A1 |
A |
17 |
O |
A1 |
A |
7 |
I |
A2 |
M |
18 |
O |
A2 |
B |
8 |
I |
A2 |
A |
19 |
O |
A2 |
M |
9 |
I |
N |
B |
20 |
O |
A2 |
A |
10 |
I |
N |
M |
21 |
O |
N |
B |
11 |
I |
N |
A |
22 |
O |
N |
M |
|
|
|
|
23 |
O |
N |
A |
Las reglas están almacenadas en la máquina de inferencia también conocida como centro de control, pues en ella se encuentran las órdenes que se deben operar. Para modelar la ANFIS se utilizó el Toolbox Fuzzy de Matlab. Seleccionamos los valores que serán procesados en las entradas Hora y Estación del Año, que pasan al fuzzificador, este lo traduce en un lenguaje comprensible para el motor de inferencia, el cual asocia cada entrada a un conjunto difuso devolviendo como salida un valor numérico y no difuso.
- Experimento y resultados
Para obtener las funciones de pertenencia de los conjuntos difusos de la velocidad del viento, temperatura, humedad relativa y radiación solar se procedió a la recopilación de datos diarios de las variables anteriores en un periodo determinado por medio de CONAGUA, a través del Servicio Meteorológico Nacional, así como el uso de indicadores climatológicos de la zona de estudio donde el clima predominante es templado semiseco. Esto también permitió obtener valores medios anuales de cada una de las variables para generar los rangos de cada conjunto difuso, y de esa manera descartar valores fuera de rango.
Las EMAs realizan recopilación y monitoreo de variables meteorológicas para generar archivos en promedio cada 10 minutos de todas las variables, esta información es enviada vía satélite en intervalos de 1 a 3 horas por estación. Los datos de las estaciones se presentan en tres formatos de acuerdo con la periodicidad en la toma de datos de las estaciones. El reporte de una hora corresponde al periodo de 10 minutos, el de 24 horas al periodo de 60 minutos y el reporte de 90 días es el correspondiente periodo de 24 horas, con lo cual obtenemos 144 registros de cada variable meteorológica.
Para la investigación se considera resolver la problemática de datos meteorológicos perdidos en los reportes de una hora, ya que son estos los que presentan mayor ausencia de datos, y entonces poder calcular la ETo para periodos horarios.
Se realizó el entrenamiento de la red neurodifusa para cada una de las variables meteorológicas, el cual consiste en un mínimo de épocas (número de iteraciones) para el procesamiento de las muestras elegidas. Dichas muestras varían de tamaño de acuerdo al número de reglas para cada variable meteorológica, las cuales se mencionaron en el apartado anterior, así como de la estación del año en cuestión. La evaluación de cada una de las redes se realizó con datos de un día para la estación invierno (día 8) que corresponde al 28 de diciembre, así como para la estación otoño (día 279) que corresponde al 25 de septiembre. Los datos para el entrenamiento fueron seleccionados de acuerdo a la formulación de cada regla en el transcurso del día evaluado.
Las tablas V y VI muestran algunas particularidades que se fueron observando con el entrenamiento de la red neurodifusa. Los datos en el transcurso del día son 144 por cada variable meteorológica; sin embargo, dicho número puede variar según las fallas de la estación; las reglas difusas como se mencionó anteriormente varían con respecto al transcurso de cada estación del año. El total de datos para el entrenamiento se obtiene del número de épocas por el número de reglas difusas para cada variable meteorológica. Los elementos de entrenamiento corresponden a aquellos registros duplicados o de relleno de días anteriores o posteriores que nos permitieron satisfacer las reglas difusas para el día evaluado. Los datos reales indican el número de datos precisos que satisfacen el entrenamiento de la red neurodifusa en el número de iteraciones correspondiente, además puede notarse que no están distribuidos equitativamente dentro de cada conjunto difuso de la variable Hora.
Tabla V. Entrenamiento de la red neurodifusa con 5 épocas
5 Épocas |
|
Día 279 Otoño |
Día 8 Invierno |
Variable Meteorológica |
VELS |
TEMP |
HR |
RAD-SOL |
VELS |
TEMP |
HR |
RAD-SOL |
Datos en el transcurso del día |
144 |
144 |
144 |
144 |
144 |
144 |
144 |
144 |
Reglas Difusas |
13 |
12 |
13 |
12 |
13 |
14 |
15 |
11 |
Elementos en el Entrenamiento
(datos faltantes rellenados por duplicidad o relleno de datos anterior o posterior) |
17 |
27 |
25 |
18 |
25 |
35 |
45 |
15 |
Datos reales
(satisficieron las reglas) |
48 |
33 |
39 |
42 |
38 |
35 |
30 |
40 |
Total de Datos de entrenamiento
(época * n de reglas) |
65 |
60 |
65 |
60 |
65 |
70 |
75 |
55 |
Tabla VI. Entrenamiento de la red neurodifusa con 10 Épocas
10 Épocas |
|
Día 279 Otoño |
Día 8 Invierno |
Variable Meteorológica |
VELS |
TEMP |
HR |
RAD-SOL |
VELS |
TEMP |
HR |
RAD-SOL |
Datos en el transcurso del día |
144 |
144 |
144 |
144 |
144 |
144 |
144 |
144 |
Reglas Difusas |
13 |
12 |
13 |
12 |
13 |
14 |
15 |
11 |
Elementos en el Entrenamiento
(datos faltantes rellenados con relleno de datos anterior o posterior) |
47 |
55 |
61 |
51 |
60 |
72 |
92 |
39 |
Datos reales
(satisficieron las reglas) |
83 |
65 |
69 |
69 |
70 |
68 |
58 |
71 |
Total de Datos de entrenamiento
(época * n de reglas) |
130 |
120 |
130 |
120 |
130 |
140 |
150 |
110 |
Como se mostró en las tablas anteriores, el número de elementos del entrenamiento no se compara con el total de datos para el entrenamiento en ambas tablas, eso significa que aunque se aumente el número de datos para el entrenamiento, una parte mínima corresponde a datos reales. De igual manera, aunque se pasó de 5 a 10 épocas los datos reales de la tabla V no se duplicaron en la tabla VI correspondiente a las 10 épocas, esto debido a dos factores principales: a que el día no satisface por completo la reglas difusas además de que el rango que comprende a cada conjunto difuso de la variable Hora (Madrugada, Mañana, Mediodía, Atardecer, Anochecer y Noche) es distinto, lo que origina variación en los datos reales en el entrenamiento en cada iteración. Por tal motivo, los rellenos de espacio que no se cubren en cada iteración del entrenamiento se hacen tomando en consideración datos que estén más próximos al día evaluado, que pueden ser días posteriores o anteriores según sea el caso, o de igual forma repetir un dato en una iteración.
Por lo tanto, el entrenamiento y validación de cada red neurodifusa se hizo con el día 279 para la estación otoño y el día 8 para la estación invierno. El desempeño de cada red se hizo con la raíz cuadrada del error cuadrático (RMSE, ver tabla VII) calculada mediante la siguiente ecuación 6.
RMSE =  (6)
(6)
Donde N es el número de observaciones consideradas, xi es el valor real y yi es el valor estimado por el modelo. En la tabla VII se pueden observar los datos obtenidos con el entrenamiento de la red neurodifusa para 5 y 10 épocas.
Tabla VII: resultados obtenidos con la red neurodifusa
|
VELS |
TEMP |
HR |
RAD-SOL |
Datos evaluados en el transcurso del día |
144 |
144 |
144 |
144 |
Rango de Hora de día |
0:00-23:50 |
0:00-23:50 |
0:00-23:50 |
0:00-23:50 |
Valor para estación del año |
otoño |
otoño |
otoño |
otoño |
Rango de valores para la variable |
0-27 Km/h |
0-26 º C |
0-100 % |
0-900Wm2 |
|
Día 279 Otoño |
RMSE con 5 épocas de entrenamiento |
2.06 |
0.95 |
1.97 |
381.61 |
RMSE con 10 épocas de entrenamiento |
2.05 |
0.53 |
1.89 |
92.53 |
Diferencia en precisión |
0.01 |
0.42 |
0.08 |
289.08 |
|
Día 8 Invierno |
RMSE con 5 épocas de entrenamiento |
2.37 |
2.98 |
3.60 |
46.48 |
RMSE con 10 épocas de entrenamiento |
1.43 |
0.88 |
2.35 |
44.84 |
Diferencia en precisión |
0.94 |
2.1 |
1.25 |
1.64 |
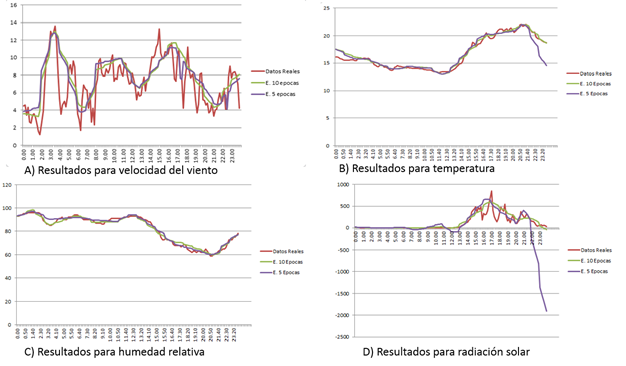
De acuerdo con los resultados obtenidos para las variables meteorológicas se muestra una mejoría al aumentar el número de épocas pues con 10 épocas se redujo el error RMSE. Respecto al comportamiento de las variables, se puede observar con claridad una mejoría en el ajuste de los datos estimados con 10 épocas con respecto a los datos reales puesto que las líneas en la gráfica muestran varias secciones de coincidencia. Ver figura 3.

Figura 3: Resultados para: A) velocidad del viento, B) temperatura, C) humedad relativa, D) radiación solar
Para valorar la utilidad de la red neurodifusa en la estimación de la evapotranspiración de referencia se procedió a su estimación siguiendo los procedimientos para periodos de tiempos horarios que señala Allen (2006), quien explica que al aplicar la ecuación FAO Penman-Monteith para periodos de tiempo horarios o menores, la ecuación y algunos procedimientos para calcular datos meteorológicos se deben ajustar para dichos periodos, por lo que la ecuación FAO Penman-Monteith para cálculos horarios se modifica de la siguiente manera:
ETo= (0.408 ∙ ∆ ∙ (Rn-G)+y∙37/(Thr+273)∙u2∙ (e° (Thr)-ea))/(∆+ γ ∙ (1+0.34 ∙ u2) (7)
Donde:
ETo evapotranspiración de referencia [mm hora-1]
Rn radiación neta en la superficie del cultivo [MJ m-2 hora-1],
G flujo del calor de suelo [MJ m-2 hora-1]
Thr temperatura media del aire a cada hora [°C]
Δ pendiente de la curva de presión de saturación de vapor en Thr,
γ constante psicrométrica [kPa °C-1],
e°(Thr) presión de saturación de vapor a temperatura del aire Thr,
ea promedio horario de la presión real de vapor [kPa],
u2 promedio horario de la velocidad del viento [m s-1]
Con la fórmula modificada para periodos horarios se calcula la ETo con datos horarios en periodos de luz de las 8:00 a las 19:00 horas de los días 25 de septiembre (día 279 otoño) y 28 de diciembre de 2013 (día 8 de invierno) en Chapingo situado a 19° 50’ latitud norte y 98° 88’ longitud oeste y 2800 m sobre el nivel del mar.
En la tabla VIII se muestran los resultados obtenidos con datos reales y datos estimados del día 25 de septiembre, que comprende el periodo 8:00 hasta las 18:00 horas del día en intervalos de una hora.
Tabla VIII. Cálculo del RMSE de la ETo real y estimada del 25 de septiembre y 8 de diciembre
Hora del día |
Eto Real
25 sep |
Eto Estimada
25 sep |
RMSE |
Eto Real
8 dic |
Eto Estimada
8 dic |
RMSE |
08:00 |
0.029 |
0.023 |
2.6807E-06 |
0.031 |
0.044 |
1.3919E-05 |
09:00 |
0.027 |
0.039 |
1.288E-05 |
0.030 |
0.068 |
0.00013122 |
10:00 |
0.030 |
0.053 |
4.6105E-05 |
0.038 |
0.412 |
0.01269089 |
11:00 |
0.029 |
0.024 |
2.2721E-06 |
0.036 |
0.027 |
7.598E-06 |
12:00 |
0.031 |
0.028 |
6.0344E-07 |
0.047 |
0.079 |
9.5851E-05 |
13:00 |
0.087 |
0.154 |
0.00040424 |
0.221 |
0.383 |
0.00240965 |
14:00 |
0.296 |
0.293 |
1.2983E-06 |
0.702 |
0.679 |
4.9402E-05 |
15:00 |
0.340 |
0.431 |
0.0007513 |
0.927 |
0.990 |
0.00035727 |
16:00 |
0.677 |
0.707 |
8.1985E-05 |
1.198 |
1.254 |
0.00028123 |
17:00 |
0.260 |
0.288 |
7.042E-05 |
0.734 |
0.942 |
0.00395536 |
18:00 |
3.654 |
3.034 |
0.03500723 |
9.098 |
9.518 |
0.01601642 |
|
|
RMSE = |
0.19073808 |
|
RMSE = |
0.18975991 |
Dicho cálculo es importante porque con su ayuda se pueden obtener otras estimaciones importantes para la administración del agua, como es el cálculo del riego neto para los diferentes cultivos.
Por ejemplo, está la estimación del riego neto para la espinaca con datos del día 25 de septiembre (día 279 de las pruebas) y con una precipitación de 110.95 mm. El riego neto se estima con la fórmula 8:
ETc= ETo * Kc (8)
Para calcular las necesidades de riego neto (Nn) usaremos la siguiente fórmula:
(Nn) = ETc – Pe (9)
Dónde:
Kc= Coeficiente de cultivo (determinado por la fase de desarrollo del cultivo)
ETo= Evapotrasnpiración de referencia
ETc = Necesidades diarias de riego de cultivo.
Precipitación efectiva (Pe)= 0.8 P – 25
Pe = 0.8 (110.95) -25 = 63.76 mm
La tabla IX muestra la estimación de la ETo y la ETc con una Kc2, pues la espinaca para el día 25 de septiembre se encuentra en su segunda fase de desarrollo y tiene un valor de 1 y la tabla X muestra la estimación de la Necesidad de riego neto junto con el RSME.
Tabla IX. Cálculo de la evapotranspiración de cultivo
|
Datos Reales |
Datos Estimados |
Hora |
ETo |
Kc2 |
ETc |
ETo |
Kc2 |
ETc |
08:00 |
0.031 |
1 |
0.031 |
0.044 |
1 |
0.044 |
09:00 |
0.03 |
1 |
0.03 |
0.068 |
1 |
0.068 |
10:00 |
0.038 |
1 |
0.038 |
0.412 |
1 |
0.412 |
11:00 |
0.036 |
1 |
0.036 |
0.027 |
1 |
0.027 |
12:00 |
0.047 |
1 |
0.047 |
0.079 |
1 |
0.079 |
13:00 |
0.221 |
1 |
0.221 |
0.383 |
1 |
0.383 |
14:00 |
0.702 |
1 |
0.702 |
0.679 |
1 |
0.679 |
15:00 |
0.927 |
1 |
0.927 |
0.99 |
1 |
0.99 |
16:00 |
1.198 |
1 |
1.198 |
1.254 |
1 |
1.254 |
17:00 |
0.734 |
1 |
0.734 |
0.942 |
1 |
0.942 |
18:00 |
9.098 |
1 |
9.098 |
9.518 |
1 |
9.518 |
Hora |
Nn con datos reales |
Nn con datos estimados con la Red Neurodifusa |
RSME |
08:00 |
0.031 |
0.044 |
1.5364E-05 |
09:00 |
0.03 |
0.068 |
0.00013127 |
10:00 |
0.038 |
0.412 |
0.012716 |
11:00 |
0.036 |
0.027 |
7.3636E-06 |
12:00 |
0.047 |
0.079 |
9.3091E-05 |
13:00 |
0.221 |
0.383 |
0.00238582 |
14:00 |
0.702 |
0.679 |
4.8091E-05 |
15:00 |
0.927 |
0.99 |
0.00036082 |
16:00 |
1.198 |
1.254 |
0.00028509 |
17:00 |
0.734 |
0.942 |
0.00393309 |
18:00 |
9.098 |
9.518 |
0.01603636 |
|
|
RSME |
0.03601236 |
Conclusiones
Se obtuvieron resultados satisfactorios en la estimación de datos faltantes para la estación Chapingo con la implementación de la red neuro-difusa, con la cual se diseñaron diversos escenarios; por ejemplo, el diseño de una red neuro-difusa formulando conjuntos difusos para el periodo de un día, un mes y un año. Este último generó mejores resultados (el que se presenta en la investigación) porque se reduce el número de conjuntos difusos y los datos para el entrenamiento se pueden adecuar con días anteriores y posteriores. Para el periodo de un mes debería crearse un mayor número de conjuntos difusos, lo que origina la problemática de ordenar los datos para cumplir cada una de las reglas, además se debe considerar que en un lapso entre los meses hay semejanza en el comportamiento de las variables.
Después de la implementación de la red neuro-difusa se obtuvieron resultados precisos con el aumento de iteraciones en el entrenamiento de la red; sin embargo, cabe aclarar que hay una posibilidad de que no solo fuera el número de iteraciones sino que al transcurrir cada iteración los datos ingresados al entrenamiento satisfagan cada una de las reglas difusas. De esa manera se evitaba la duplicidad de datos en iteraciones posteriores, lo que conlleva a una buena distribución de datos dentro del entrenamiento.
La propuesta de este trabajo consiste en probar el modelo basado en redes neuro-difusas para el relleno de datos debido a su capacidad de resolver problemas relacionados con la incertidumbre de la información o conocimiento de los expertos. Así, la red neuro-difusa se considera una buena opción en función del tipo de datos disponibles y del formato en que se publican (formato de archivos Excel).
Nuestro modelo puede mejorar si se cuenta con un historial de registros de años anteriores, así se anexaría como nueva entrada el año en estudio en la red, lo que permitiría comparar datos de años anteriores o predecir datos a futuro.
También se puede mejorar el desempeño de la red mediante un sistema que pueda generar los datos de entrenamiento de forma automatizada ya que en la investigación se realizó de forma manual, esto facilitaría la retroalimentación a la red, así como establecer un punto en el cual pueda ocurrir un sobre entrenamiento. Aunque la lógica difusa tiene una historia corta, es una técnica prometedora en el campo de recuperación de información meteorológica.
Bibliografía
Alfaro, J., & Javier, F. (2008). Descripción de dos métodos de rellenado de datos ausentes en series de tiempo meteorológicas. Revista de Matemática: Teoría y Aplicaciones, 60-758.
Alfaro, J., & Soley, J. (2009). Descripción de dos métodos de rellenado de datos ausentes en series de tiempo meteorológicas. Revista de Matemática: Teoría y Aplicaciones.
Arca, B. B. (2001). Evaluation of neural network techniques for estimating evapotranspiration. En Evolving Solution with Neural Networks, Italia: Baratti, R. y De Canete, pp. 62-97.
Campos, A., Quispe, S., & Tatiana, S. (2012). Gestión de datos meteorológicos. XXII Congreso Nacional de Hidráulica. Acapulco Guerrero.
Chen, H. (1995). Machine learning for information retrieval: neural networks, symbolic learning, and genètic algorithms. Journal ofthe American Soclety for Information Science.
Cruz, H. (2012). Estimación de la evapotranspiración de referencia en regiones con datos climáticos limitados. Texcoco.
Doorenbos, J., & Pruitt, W. (1997). Guidelines for predicting crop water requirements. Rome: Irrigation and Drainage Paper.
Elizondo, D. G. (1994). Development of a neural network model to predict daily solar radiation. Agricultural and Forest Meteorology, pp. 115-132.
Enke W, S. A. (1997). Downscaling climate model outputs into local and regional weather elements by classification and regression. Climate Research, pp. 195-207.
Ferreira, M. (2003). Metodologías de análisis e imputación de datos faltantes en series de velocidad del viento. VI Congreso Galego de Estatística e Investigación de Operaciónes, pp. 5-7.
Jang., J. S. (1993). ANFIS: adaptive-network-based fuzzy inference system. IEEE Transactions on Systems, pp. 665-685.
JE, K. (2001). Empirical eigenvectors of sea-level pressure, surface temperature and precipitation complexes over North America. Cagliari.
Lin, C., Lee, T., & CS, G. (1996). Neural Fuzzy System: A Neuro-Fuzzy Synergism to Intelligent Systems. Prentice Hall.
M. del Brio Bonifacio, S. M. (2010). Redes Neuronales y Sistemas Borrosos. Madrid. España: Alfaomega.
Pitarque, A., & Roy, J. (1998). Redes neuronales vs modelos estadísticos: Simulaciones sobre tareas de predicción y clasificacíon, Valencia, España: Universidad de Valencia, pp. 387-400..
R. Alfaro, R. P., Alfaro, R., & Pacheco, R. (2000). Aplicación de algunos métodos de relleno a series anuales de lluvia de diferentes regiones de Costa Rica. Redalyc.
Rivera, M. (2008). Estimación estadística de valores faltantes en series históricas de lluvia. Pereira: Facultad De Ingeniería Industrial, Escuela de Posgrados.
Saba, I., & Ortega, J. (2008). Estimación de datos faltantes en estaciones meteorológicas de Venezuela vía un modelo de redes neuronales.
Solana, H., & Bote, G. (1998). La aplicación de Redes Neuronales Artificiales (RNA): a la recuperación de la información.
Valesani, E., & Quintana, P. (2009). Imputación de datos con redes neuronales. XI Workshop de Investigadores en Ciencias de la Computación, Argentina, pp. 281-285.
Villada F, & García, E. (s.f.). Pronóstico del Precio de la Energía Eléctrica usando Redes Neuro-Difusas. Redalyc.
Wilby R, W. T. (1997). Downscaling general circulation model output: a review of methods and limitations. Progress in Physical Geography, pp. 530-548.